Esercizio sul teorema di Norton
Esercizio svolto sul teorema di Norton
Dato il seguente circuito determinare la corrente che scorre nella resistenza R6 cioè IR6.
Si sappia che:
R1 = R2 = R3 = R4 = R5 = R6 = 100 Ω
e che:
E1 = E2 = 5 V

Svolgimento dell'esercizio
Applichiamo il teorema di Norton al circuito elettrico proposto. Scegliamo i due morsetti A e B ai capi del resistore 6:

Per cui il circuito da ridurre a generatore reale di corrente è:
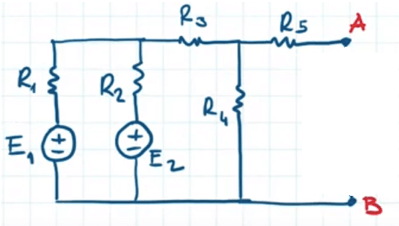
Calcoliamo la IN e la RN del bipolo equivalente di Norton.
Per calcolare la resistenza equivalente del bipolo, non essendo presenti generatori ideali di corrente da aprire, annulliamo soltanto contemporaneamente tutti i generatori ideali di tensione cioè cortocircuitiamoli.

Calcoliamo adesso la resistenza equivalente di questo circuito semplificato. Le resistenze R1 ed R2 sono in parallelo quindi la loro resistenza equivalente R12 vale:
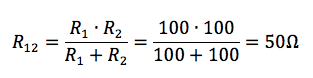
Il parallelo di R1 e R2 è collegato in serie con R3 per cui la loro resistenza equivalente R12-3 vale:
![]()
Questa resistenza R12-3 è collegata a sua volta in parallelo con R4, per cui:
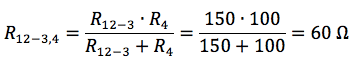
Infine quest'ultima resistenza è in serie con R5 per cui la resistenza complessiva di Norton RN varrà:
RN = R12-3,4 + R5 = 60 Ω + 100 Ω = 160 Ω
Per determinare la corrente tra i morsetti A e B li cortocircuitiamo:

L'obiettivo è calcolare la IN ovvero la corrente di cortocircuito che scorre tra i morsetti A e B. Applichiamo allora il teorema di Thevenin scegliendo opportunamente altri due morsetti C e D che semplificano il circuito in questo modo:

La resistenza equivalente di Thevenin ai morsetti C e D si calcola annullando contemporaneamente i generatori ideali E1 ed E2 per cui R1 ed R2 rimangono collegati in parallelo:
Rth = 50 Ω
Per la tensione di Thevenin tra i morsetti C e D consideriamo la maglia:
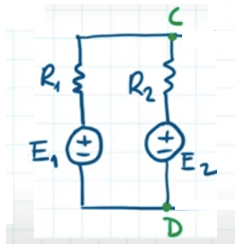
Applichiamo la legge delle maglie di Kirchhoff e segniamo i versi delle tensioni prendendo come positivo il verso orario:
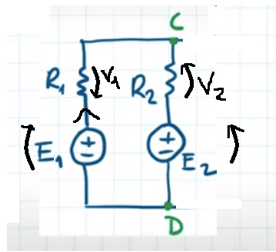
La somma delle tensioni nella maglia è:
E1 – V1 – V2 – E2 = 0
Ma essendo le resistenze identiche ed entrambe collegate ad un generatore che eroga la stessa tensione saranno attraversate dalla stessa corrente i:
E1 – i ∙ R1 – i ∙ R2 – E2 = 0
Quindi la corrente che scorre nella maglia è

Per cui tra i morsetti C e D vi è solo come contributo in termini di tensione di E2 = 5 V
ECD = Eth = 5 V.
Semplifichiamo dunque il circuito ai morsetti C e D inserendo il bipolo che rappresenta un generatore reale di tensione:
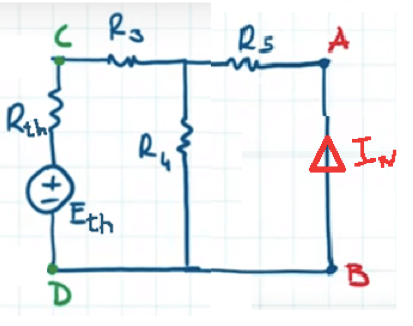
Le resistenze R4 ed R5 risultano connesse in parallelo e il loro equivalente vale
R45 = 50 Ω
La resistenza equivalente è dunque pari alla somma delle tre resistenze in serie Rth, R3 ed R45:
Re = 50 Ω + 100 Ω + 50 Ω = 200 Ω
La corrente i che scorre nell'equivalente è
i = Eth / Re = 5 / 200 = 0,025 A
La caduta di tensione ai capi di R45 è
V45 = R45 ∙ i = 50 ∙ 0,025 = 1,25 V
Le resistenze R4 ed R5 risultando connesse in parallelo avranno entrambe allora caduta di tensione pari a 1,25 V. La corrente che scorre in R5 sarà quella che passa nel cortocircuito tra A e B:
IN = V5 / R5 = 1,25 / 100 = 0,0125 A
che rappresenta appunto la corrente erogata dal generatore ideale di corrente di Norton.
Torniamo adesso al circuito originario sostituendo il bipolo di Norton (generatore ideale di corrente con IN = 0,0125 A in parallelo a RN = 160 Ω) ai morsetti A e B:
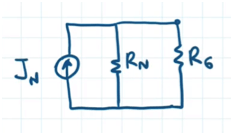
La resistenza equivalente del circuito vale:
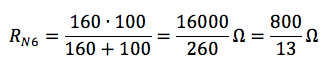
La caduta di tensione ai capi di questa resistenza equivalente è:
V = RN-6 ∙ IN = (800/13) ∙ 0,0125 = 0,769 V = VN = V6
Che è anche la caduta di tensione ai capi di R6 essendo in parallelo con RN e quindi la corrente che scorre in R6 vale:

Link correlati:
Che cosa afferma il teorema di Tellegen?
Esercizio svolto sul teorema di Thevenin
Esercizio su resistori in parallelo
Collegamento di resistenze in serie
Che cos'è un circuito RC?
Studia con noi