Esercizio sul teorema di Thevenin
Esercizio svolto sul teorema di Thevenin
Dato il seguente circuito calcolare la corrente che scorre nella resistenza R4 cioè la IR4.
I dati sono:
E1 = 100 V; R1 = 10 Ω; R2 = 20 Ω; R3 = 5 Ω; R4 = 30 Ω; R5 = 15 Ω; E2 = 80 V

Svolgimento dell'esercizio
Isoliamo la parte di circuito che vogliamo trattare col teorema di Thevenin. Poiché il problema ci chiede la corrente che scorre nella resistenza 4 conviene scegliere i morsetti A e B prima di R4 e dopo R5 rispettivamente:

Il circuito si riduce a:

Calcoliamo la resistenza equivalente Rth del bipolo equivalente. Annulliamo E1 e quindi le due resistenze R1 ed R2 saranno in parallelo tra di loro e il loro parallelo sarà collegato in serie con R3 ed R5.
Calcoliamo la resistenza equivalente. Chiamami R1,2 la resistenza equivalente del parallelo delle due resistenze R1 ed R2:
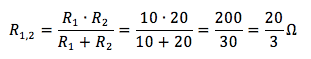
Per cui la resistenza equivalente è la somma di quest'ultima con la quinta e la terza resistenza:
Rth = Re = R1,2 + R3 + R5 = 20/3 + 5 + 15 = 20/3 +20 = 80/3 Ω ≈ 26,7 Ω
Calcoliamo adesso la tensione a vuoto Eth del bipolo equivalente. "Tensione a vuoto" vuol dire che nei morsetti A e B non circola corrente. Essendo la corrente nulla nei due morsetti sulla resistenza 3 e sulla resistenza 5 non ci sarà alcuna caduta di tensione quindi è come se non ci fossero per il calcolo della tensione tra i due morsetti:

La tensione tra i morsetti dunque è equivalente alla tensione ai capi della resistenza R2. La serie tra le due resistenze 1 e 2 collegate in serie è:
R1,2 = R1 + R2 = 10 + 20 = 30 Ω
La corrente che circola attraverso queste due resistenze in serie è pari a:
i1,2 = E1 / R1,2 = 100 / 30 = 10/3 Ω
La caduta di tensione ai capi della resistenza 2 dunque sarà:
VR2 = i1,2 ∙ R2 = (10/3) ∙20 = 200/3 V ≈ 66,7 Ω
Quindi la tensione di Thevenin del bipolo equivalente è:
Eth = 66,7 V
Allora il circuito isolato all'inizio è equivalente ad un semplice bipolo così fatto:
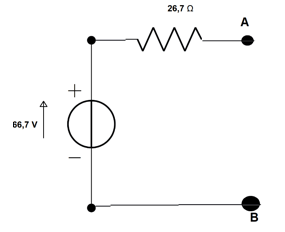
Riprendiamo il circuito iniziale con la resistenza 4 e il generatore E2 e colleghiamolo ai morsetti A e B:
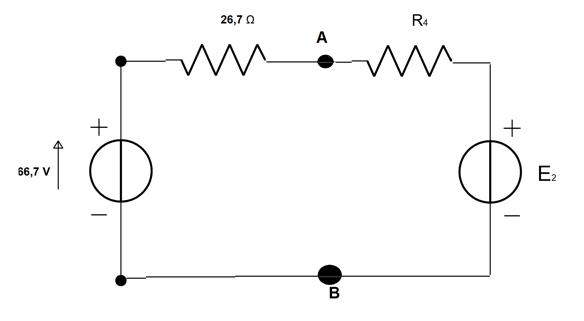
La corrente che scorre nell'unica maglia del circuito è uguale sia per la resistenza Rth sia per la resistenza R4. Applichiamo la legge delle maglie al circuito scegliendo come verso positivo quello orario.
Essendo E2 > E1 la corrente circolerà uscendo dal polo + di E2 e secondo le convenzioni viste per le leggi di Kirchhoff:
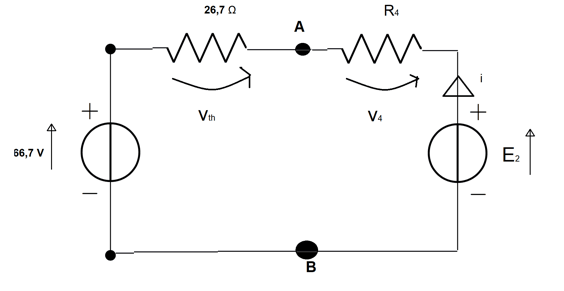
Allora l'equazione della maglia è:
Eth + Vth + V4 – E2 = 0
Eth + i∙ Rth + i ∙ R4 – E2 =0
Raccogliendo la i:
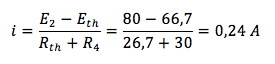
Link correlati:
Che cosa afferma il teorema di Tellegen?
Che cosa afferma il teorema di Norton?
Che cos'è la reattanza?
Studia con noi