Applicazione della forza di Lorentz
Esercizio con applicazione della forza di Lorentz
Un campo magnetico di intensità 1 T ortogonale al foglio viene investito da un protone avente un'energia pari a 6 MeV.
La traiettoria del protone forma un angolo di 30° con l'asse orizzontale.
Il protone esce da tale regione dopo aver percorso una distanza orizzontale d e con un certo angolo di inclinazione.
Calcolare l'angolo di uscita dall'asse orizzontale e la distanza percorsa tra ingresso ed uscita.

Svolgimento
Dal testo del problema si evince che esiste una regione di spazio in cui è presente un campo magnetico entrante nel foglio ed ortogonale ad esso, che viene attraversato da un protone dotato di una certa energia cinetica e quindi di una data velocità V.
Tale velocità risulta inclinata di un angolo α rispetto all'asse orizzontale.
Il testo del problema dice che il protone riemerge dalla regione in cui è presente il campo dopo una certa distanza d rispetto al punto di ingresso.
Ciò vuol dire che la carica non possiede sufficiente energia (e quindi velocità idonea) per rimanere confinata nella regione magnetica, ma riemerge sfuggendo alle forze del campo.
Sulla carica agirà la forza di Lorentz che controbilanciando la forza centripeta, darà luogo ad un moto circolare della carica.
Si chiede dapprima di determinare l'angolo di uscita dopo essere penetrato all'interno del campo ed essere riemerso.
Certamente il protone descriverà soltanto un arco di circonferenza e non un'intera circonferenza visto che riemerge.
Dunque per questione di simmetria, l'angolo di inclinazione della velocità in uscita rispetto al piano orizzontale sarà il medesimo di quello di entrata:
α = α'
Ora scriviamo i dati forniti dal problema:
B = 1 T
α = 30°
E = 6 MeV = 6 ·106 eV = 6 · 1,6 ·10-16 J = 9,6 ·10-16 J
mp = 1,67 ·10-27 kg (massa del protone)
q = 1,6 ·10-19 C (carica del protone)
Ora la forza di Lorentz eguaglierà la forza centripeta che permette il moto circolare per cui:
Florentz = Fcentripeta
Da cui
q · V · B · senα = m · V2 / R
in cui
- q è la carica della particella
- V la sua velocità
- B l'intensità del campo magnetico
- α l'angolo tra V e B
- m la massa della particella
- R il raggio della traiettoria circolare.
L'energia di 6 Mev corrisponde all'energia cinetica K, per cui:
E = K = ½ · m · v2
Da cui:
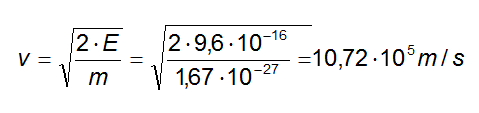
Ricaviamo dunque il raggio della traiettoria:
R = (m · V)/( q · B · sen α)
Ovvero:
R = (1,67 ·10-27 · 10,72 · 105) / (1,6 ·10-19 · 1 · sen30) = 22,4 ·10-3 m = 22,4 mm
Ora poiché il protone percorre solo un arco di circonferenza utilizziamo il teorema della corda per calcolare la distanza orizzontale:
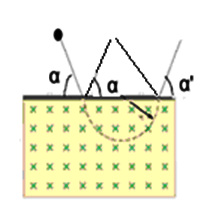
I due segmenti disegnati che partono rispettivamente dal punto di ingresso della carica e da quello di uscita, convergono entrambi ad un unico punto, che si trova sull'altro lato della circonferenza se questa fosse tutta completa.
L'unica parte di questa circonferenza evidenziata è quella tratteggiata e corrisponde proprio alla trattoria seguita dal protone.
Per il teorema della corda, la lunghezza della corda (distanza incognita da determinare) è dato dal prodotto del diametro per il seno dell'angolo alla circonferenza che in questo caso è proprio α:
d = 2 · R · sen α = 2 · 22,4 · sen30 = 22,4 mm (22,4 millimetri)
Dunque la distanza orizzontale percorsa dal protone prima di riemergere dal campo è di 22,4 mm.
Studia con noi