Come varia l'accelerazione di gravità con l'altezza
Valore dell'accelerazione di gravità e quota
Il valore dell'accelerazione di gravità è indipendente dalla massa del corpo considerato, quindi ogni corpo è soggetto alla medesima accelerazione, così come scoperto da Galileo Galilei (questo nel caso in cui la resistenza dell'aria risulta trascurabile).
Invece il valore di g può essere considerato costante e pari con una buona approssimazione a 9,8 m/s2 solo se la quota h considerata a partire dalla superficie terrestre è trascurabile rispetto alle dimensioni del raggio della Terra.
Non è più legittimo ritenere tale valore costante se la quota di altezza diventa considerevole, come ad esempio nel caso del volo di un missile spaziale.
In generale g diminuisce all'aumentare dell'altezza h, ma vediamo questo concetto nel dettaglio.
Calcolo del valore dell'accelerazione di gravità in funzione dell'altezza
Consideriamo un oggetto posto ad una certa altezza h sopra la superficie della Terra.
La distanza tra l'oggetto e il centro del pianeta è:
d = R + h
in cui R è il raggio della Terra:

L'accelerazione con cui il corpo, lasciato libero di cadere, incrementa la propria velocità vale:

e sarà funzione dell'altezza h.
(Per approfondimenti su questa formula si veda quanto esposto relativamente alla accelerazione di gravità).
Se h risulta molto inferiore al raggio terrestre
h << R
allora il termine al denominatore riscritto come:
1/(R + h)2 = (R + h)-2
può essere approssimato ricorrendo al binomio di Newton secondo la logica che segue:

in cui:
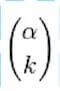
è il coefficiente binomiale che si può calcolare come

Ora nel nostro caso il termine (R+h)-2 va riscritto nella forma (1 + x)α, per cui raccogliamo il termine R all'interno della parentesi:
(R+h)-2 = [R · (1 + h/R)]-2 = R-2 · (1 + h/R)-2
Applichiamo ora la formula del binomio di Newton considerando x = h/R ed α = -2:
R-2 · (1 + h/R)-2 = R-2 · (1 - 2 · h/R + . . .)
Ci fermiamo al termine di primo grado che rappresenta giù un'ottima approssimazione.
Allora l'accelerazione di gravità g varrà:

Ma il termine (G · MT / R2) vale proprio g:
g = (G · MT / R2)
Per cui:

La variazione di accelerazione di gravità tra il valore a livello della superficie terrestre (9,8 m/s2) ed il valore di g ad una certa quota h vale dunque:
Δg = g(h) - g = g · (1 - 2 · h/R) - g = g - 2 · g · h/R - g = - 2 · g · h/R
Il segno meno sta a significare che g decresce quando h cresce, così come la logica porta a pensare (più si ci allontana dalla superficie, meno intensa sarà l'accelerazione di gravità).
Ora per un'altezza di 100 km (100000 m =105 m) dalla superficie del nostro pianeta, la variazione di g sarà:
Δg = - 2 · g · h/R = -2 · 9,8 · 105 /(6,38 · 106) = - 0,3 m/s2
Dunque l'accelerazione di gravità a 100 km varrà:
g(100 km) = 9,8 - 0,3 = 9,5 m/s2
con una variazione percentuale di appena il 2%.
Ci si convince dunque che nei comuni fenomeni considerati in meccanica l'approssimazione di considerare g costante a 9,8 m/s2 risulta più che ottima.
La seguente tabella mostra i valori dell'accelerazione di gravità man mano che aumenta l'altitudine fino a 100 km:

Esercizio
A quale altezza rispetto al suolo terrestre bisognerebbe portare un corpo affinché si dimezzi il peso?
Lo svolgimento dell'esercizio lo trovi qui: altezza dal suolo per dimezzare la forza peso.
Esercizio sul calcolo dell'accelerazione di gravità
Calcolare a quale valore dell'accelerazione di gravità è sottoposto un satellite in orbita circolare a 160 km di altezza dalla superficie terrestre.
Lo svolgimento dell'esercizio lo trovi qui: esercizio sul calcolo dell'accelerazione di gravità.
Esercizio sulla accelerazione di gravità in funzione della altezza
Calcolare la variazione del valore dell'accelerazione di gravità per un'altezza di 200 km a partire dal livello del mare e determinarne il valore a tale quota.
La soluzione dell'esercizio la trovi qui: esercizio sulla accelerazione di gravità in funzione della altezza.
Link correlati:
Come funziona un missile balistico?
Studia con noi