Trasformazione adiabatica su gas perfetto monoatomico
Esercizio su trasformazione adiabatica su gas perfetto monoatomico
Un cilindro del volume di 3,0 L contiene un gas perfetto monoatomico alla pressione di 1,2∙105 Pa.
Successivamente a una trasformazione adiabatica la pressione diminuisce del 30% rispetto al valore iniziale mentre la temperatura risulta 310 K.
Calcolare il volume finale del gas e il numero di moli contenute nel cilindro.
Stabilire infine se il gas si è raffreddato o riscaldato rispetto alla temperatura iniziale.
Svolgimento dell'esercizio
Le condizioni iniziali di pressione e volume del gas sono:
Pi = 1,2 ∙ 105 Pa
Vi = 3,0 L = 3,0 ∙ 10-3 m3
Mentre le condizioni finali di pressione e temperatura del gas sono:
Pf = Pi - 30% Pi = (1 - 0,3) ∙ Pi = 0,7 ∙ 1,2 ∙ 105 Pa = 0,84 ∙105 Pa
Tf = 310 K
L'equazione associata a questa trasformazione adiabatica è l'equazione di Poisson:
P ∙ Vγ = cost
in cui P è la pressione, V il volume del gas e γ (gamma) è il rapporto fra il calore specifico a pressione costante del gas e quello a volume costante che in questo caso essendo il gas monoatomico vale 5/3. Dunque:
Pi ∙ Viγ = Pf ∙ Vfγ
Da cui possiamo ricavare il valore del volume finale:
Vfγ = Pi ∙ Viγ / Pf
Sostituendo i dati in nostro possesso si ha che:
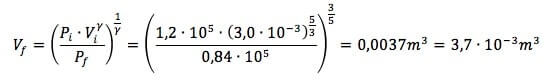
Per determinare il numero di moli sfruttiamo l'equazione di stato dei gas perfetti:
P∙V = n∙R∙T
in cui n è il numero di moli che risultano allora pari a:

Trattandosi di un'espansione adiabatica (il volume è infatti passato da 3 litri iniziali ai 3,7 finali) possiamo affermare che il gas ha subito un processo di raffreddamento.
Studia con noi