Reazione vincolare di una guida
Calcolo della reazione vincolare di una guida
Un blocco di massa m = 0,5 kg è sottoposto ad una forza orizzontale F di modulo 470 N per un tempo di 0,01 s.
Il blocco si mette in moto su di un piano liscio e successivamente incontra una guida circolare anch'essa liscia di raggio 1,6 m.
Il corpo inizia così a percorrere la guida e ad elevarsi di quota.

Calcolare la reazione vincolare della guida quando l'angolo percorso è pari a 120°.
Svolgimento dell'esercizio
Il problema della guida circolare è un tipico esempio di situazione fisica risolvibile a partire dalla legge di conservazione dell'energia meccanica.
Infatti la massa m a cui è applicata la forza F, acquisisce una certa velocità V che mantiene fino all'incontro della guida circolare, in quanto il piano è liscio.
Una volta che inizia a salire di quota lungo la guida parte dell'energia cinetica iniziale si trasformerà in energia potenziale gravitazionale.
Per cui imponendo la conservazione dell'energia meccanica tra istante in cui la massa entra nella guida e istante finale con θ = 120° possiamo ricavare la velocità tangenziale del corpo a quella quota.
Ricordando che il corpo aderisce alla guida se la forza centripeta uguaglia la forza di reazione e quella peso, è possibile ricavare la reazione.
Dalla seconda legge di Newton ricaviamo l'accelerazione impressa al corpo:
a = F / m
Tale accelerazione applicata per un intervallo Δt di tempo restituisce come velocità finale (velocità iniziale nulla):
V = a ∙ Δt = (F/m) ∙ Δt
Imponiamo che l'energia meccanica iniziale costituita esclusivamente dalla componente cinetica, sia pari alla somma di energia cinetica ed energia potenziale gravitazione alla quota a cui si porta il corpo.
In particolare la quota h a cui il corpo si porta è la somma del raggio più il prodotto di R per il seno di 30°

½ ∙m ∙V2 = ½ ∙ m ∙ V12 + m ∙ g ∙ (R + R ∙ sen30)
Semplifico m e raccolgo R
½ ∙ V2 = ½ ∙ V12 + R ∙ g ∙ (1 + sen30)
Ricordando che:
V = F/m ∙ Δt
e che sen30 = ½
Si ha che:
½ ∙ (F/m ∙ Δt)2 = ½ ∙ V12 + 3/2 ∙ R ∙ g
Moltiplichiamo per 2 ambo i membri
(F2 ∙ Δt2) / m2 = V12 + 3 ∙ R ∙ g
Ricaviamo V1:

Ora analizziamo il diagramma delle forze libere agenti sulla massa che si trova a quota h.
Le forze che agiscono sono la reazione della guida diretta verso il centro e la forza peso diretta verso il basso.
La risultante sarà il prodotto della massa per l'accelerazione centripeta ovvero la forza centripeta diretta anch'essa verso il centro.
Da un punto di vista di vettoriale deve risultare che:
R + P = Fc
Ponendoci in un sistema di riferimento con l'asse x nella stessa di direzione di R, allora la forza peso risulta avere due componenti.
In particolare la componente orizzontale è pari al prodotto di m∙g per il coseno di 60°
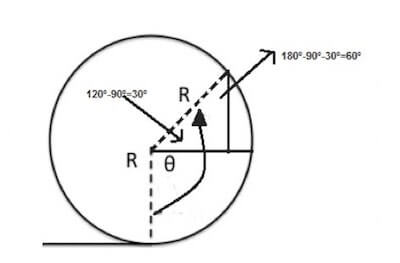
Dunque:
R + m ∙ g ∙ cos60 = m ∙ V12 / R
Da cui:
R = m ∙ V12 /R - m ∙ g ∙ cos60
Raccogliendo m si ha che:
R = m ∙ (V12 /R - g ∙ cos60)
Sostituendo i dati in nostro possesso risulta che:
R = 0,5 ∙ ( 6,432 / 1,6 – 9,8 ∙ cos60) = 10,5 N
Pertanto la reazione vincolare della guida quando l'angolo percorso è di 120° è pari a 10,5 N.
Studia con noi