Modulo, direzione e verso del campo elettrico
Calcolo del modulo, direzione e verso del campo elettrico
Tre piani paralleli isolanti, infinitamente estesi e di spessore trascurabile, sono elettricamente carichi con densità superficiale di carica σ1 = σ , σ2 = 2∙σ, σ3 = -σ.
Essi sono collocati in maniera tale che la distanza tra il primo e il secondo piano vale d, mentre quella tra il secondo e il terzo piano vale 3d.
Si determini: modulo, direzione e verso del campo elettrico nelle regioni A, B, C e D indicate in figura.
Dati numerici:
σ = 7,13∙10-9 C/m2
d = 3.01 cm

Svolgimento dell'esercizio
Il campo elettrico generato da una superficie piana infinitamente carica è pari al rapporto tra la densità superficiale di carica e due volte la costante dielettrica nel vuoto:
E = σ / (2 ∙ ε0)
Tale campo è uniforme nello spazio ovvero assume lo stesso valore indipendentemente dalla distanza dal piano.
Nella regione contrassegnata dalla lettera A i due campi E1 ed E2 generati rispettivamente dai due piani carichi positivamente 1 e 2 avranno verso uscente dai rispettivi piani e quindi i due vettori saranno orientati verso sinistra.
Il campo E3 generato dal piano n 3 carico negativamente avrà invece il verso entrante diretto al piano 3.

Stabilendo come positivo l'orientamento verso destra dell'asse orizzontale, allora il modulo del campo elettrico risultante nella zona A sarà pari a:
EA = E3 – E1 – E2
EA = 1/(2∙ε0) ∙ (s3 - s1 - s2)
EA = 1/(2∙8,85∙10-12) ∙(7,13 - 7,13 - 2∙7,13)∙10-9
EA = - 8,06 ∙ 102 N/C
Per cui il campo nella zona A sarà rivolto verso sinistra e sarà rappresentato da linee di campo parallele.
Nella zona B il vettore E1 sarà rivolto verso destra, il vettore E2 verso sinistra e E3 verso destra:
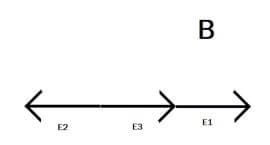
EB = E1 + E3 - E2
EB = 1/(2∙ε0) ∙ (s1 + s3 - s2)
EB = 1/(2∙8,85∙10-12) ∙(7,13 + 7,13 - 2∙7,13)∙10-9 = 0
Per cui il campo elettrico risultante nella zona B sarà nullo.
Nella zona C tutti e tre i campi sono rivolti verso destra:
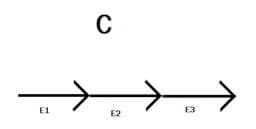
EC = E1 + E2 + E3
EC = 1/(2∙ε0) ∙ (s1 + s2 + s3)
EC = 1/(2∙8,85∙10-12) ∙ (7,13 + 2∙7,13 + 7,13)∙10-9
EC = +1,61∙103 N/C
Per cui il campo nella zona C sarà rivolto verso destra e sarà rappresentato da linee di campo parallele.
Infine nella zona D i campi E1 ed E2 saranno rivolti verso destra mentre il vettore E3 sarà rivolto a sinistra:

ED = E1 + E2 - E3
ED = 1/(2∙ε0) ∙ (s1 + s2 - s3)
ED = 1/(2∙8,85∙10-12) ∙(7,13 + 2∙7,13 - 7,13)∙10-9
ED = +8,06∙102 N/C
Per cui il campo nella zona D sarà rivolto verso destra e sarà rappresentato da linee di campo parallele.
Link correlati:
Cosa afferma il teorema di Gauss?
Esercizio svolto e commentato sul teorema di Gauss
Come può essere dimostrato il teorema di Gauss?
Principali applicazioni del teorema di Gauss?
Studia con noi