fem indotta per flusso tagliato
Calcolo della fem indotta per flusso tagliato
Una spira triangolare conduttrice reale di resistenza R, chiusa, omogenea, di lati
AC = b = 40,0 cm ; AD = h = 30,0 cm ; ipotenusa CD = d
giace in un piano riferito ad un sistema di assi cartesiani ortogonali Oxy e trasla con velocità vi costante lungo l'asse x, come in figura:
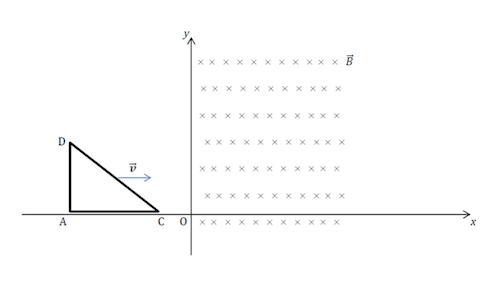
Nel punto x = 0 la spira entra in un campo magnetico B, costante e uniforme, entrante nel piano.
Si chiede di determinare la fem ℇ indotta per flusso tagliato in funzione di B, v e t (con B intensità del campo magnetico e v modulo della velocità della spira) ed in funzione di B, v e xc (con B intensità del campo magnetico, v modulo della velocità della spira e xc coordinata x del vertice C della spira triangolare) nei tre casi seguenti:
- la spira non è entrata nella zona del campo B (cioè xC < 0)
- la spira è a cavallo dell'asse y (xA < 0 < xC)
- la spira ha superato l'asse y (xA > 0)
Svolgimento dell'esercizio
La variazione di flusso tagliato del campo magnetico si verifica tutte le volte che un circuito, o una sua parte, si muove entro un campo magnetico costante ed uniforme oppure un campo magnetico si muove rispetto al circuito.
In accordo con la legge di Faraday-Neumann-Lenz sulla spira triangolare del problema si manifesterà una forza elettromotrice indotta ε proporzionale alla rapidità con cui varia il flusso di campo magnetico attraverso la superficie delimitata dal circuito.
La corrente indotta è presente fino a quando vi è una variazione di tale flusso nel tempo ed è tanto maggiore quanto più rapida è la variazione.
Il verso della corrente indotta si determina con la legge di Lenz: il verso di tale corrente è tale da produrre a sua volta un altro campo magnetico che tende ad opporsi alla variazione di flusso del campo magnetico esterno che l'ha generata. In formule:
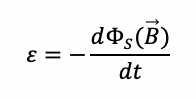
La fem indotta è cioè pari alla derivata rispetto al tempo del flusso del campo magnetico calcolato attraverso la superficie del circuito e cambiata di segno.
Nel caso in cui la coordinata x assunta dal punto C della spira sia negativa, xc < 0, cioè quando la spira non è ancora entrata nella zona del campo non si rileverà alcuna variazione di flusso di campo magnetico per cui la fem indotta sarà nulla.
Quando la spira si trova a cavallo dell'asse y cioè per xA < 0 < xC si avrà una variazione di flusso di campo magnetico e quindi si manifesterà una fem indotta. Tale fem indotta è pari a:
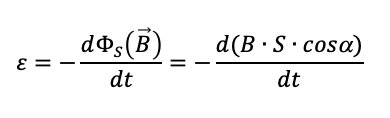
Essendo il campo entrante nel piano risulta perpendicolare alla superficie cioè parallelo al vettore normale. Per cui cosα = 1.
Inoltre il valore dell'intensità del campo magnetico è costante e quindi può essere portato fuori dall'operazione di derivata. Allora avremo che:
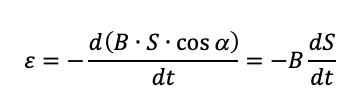
Per calcolare la superficie che risulta investita dalle linee di campo man mano che la spira avanza verso destra calcoliamo la tangente goniometrica dell'angolo γ in C del triangolo rettangolo. Sappiamo dalla trigonometria che:
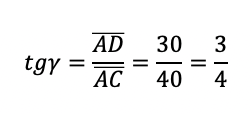
Il cateto verticale in funzione del valore che assume la coordinata xC varrà:
h(xc) = xc ∙ tg γ = ¾ ∙ xC
Allora la superficie S della porzione di triangolo rettangolo immersa nel campo magnetico in funzione della coordinata xC è:
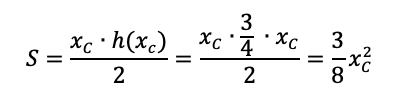
Dunque la fem indotta varrà:
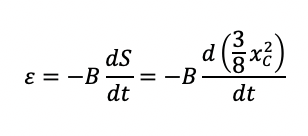
Ora xc varia nel tempo in relazione alla velocità v con cui la spira si sta muovendo secondo la legge:
xc = v ∙ t
per cui:
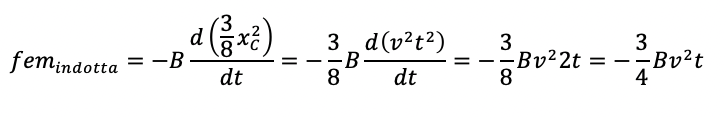
Questo andamento dura da t = 0 fino al momento in cui tutto il triangolo è entrato nel campo magnetico cioè fino a quando xc assume il valore di 40 cm (lunghezza del lato AC).
Una volta che la spira ha completamente superato l'asse y e si trova tutta immersa nel campo non vi sarà più variazione di flusso del campo magnetico e quindi la fem indotta sarà zero.
Ricapitolando quindi la fem indotta ε per flusso tagliato vale:
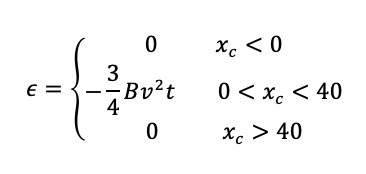
Con xc misurato in cm, B in T e v in m/s.
Sostituendo a t la sua espressione in funzione della coordinata x di C:
t = xc / v
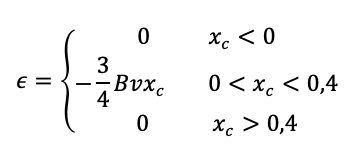
Con B misurato in T, v in m/s e xc in m.
Link correlati:
Calcolo della costante di tempo di un circuito RC
Esercizio sul calcolo della fem indotta
Esercizio su una sbarra conduttrice cilindrica che si appoggia a due rotaie
Esercizio riguardante la scarica di un condensatore carico attraverso una resistenza
Studia con noi