Sbarra conduttrice che si appoggia a due rotaie conduttrici
Esercizio su una sbarra conduttrice cilindrica che si appoggia a due rotaie conduttrici
Una sbarra conduttrice cilindrica di rame avente resistenza pari a 1,1 Ω, si appoggia a due rotaie conduttrici di resistenza trascurabile, poste su un piano orizzontale e disposte a formare tra loro un angolo α = 45°.
La sbarra, partendo dal punto O di incrocio delle rotaie (vedi figura), viene fatta muovere lungo l'asse x per mezzo di una forza esterna F. Perpendicolarmente al piano delle rotaie è presente un campo magnetico B = 1 T, uscente
rispetto al piano della figura. Il moto risultante avviene con velocità costante v.
Se la fem instaurata nel circuito quando la sbarra si trova nella posizione x1= 0.5 m rispetto all'incrocio delle rotaie è pari a ℰ1 = 0,2 V determinare, in funzione della posizione x della sbarra:
- la velocità della sbarra;
- la corrente che circola nel circuito nell'istante in cui x1 = 0,5 m.

Svolgimento dell'esercizio
Il circuito descritto dal problema è composto da due lati fissi (ipotenusa e cateto orizzontale) ed un cateto mobile (cateto verticale) che sta traslando verso destro a velocità costante v.
Poiché la superficie del circuito immersa nel campo magnetico presente in questo piano sta aumentando si verificherà anche una variazione del flusso del campo magnetico concatenato alla superficie racchiusa dal circuito e quindi si manifesteranno una fem ed una corrente indotta nel circuito.
In particolare detta x la posizione della sbarretta mobile rispetto al punto O la velocità con cui questa si muove è data da:
v = x / t
Questa espressione restituisce la velocità in funzione della posizione x e del tempo t.
Vogliamo un'espressione in cui compaia solo la posizione x della sbarra rispetto all'origine.
La fem indotta, in valore assoluto, nel circuito applicando la legge di Faraday Neumann Lenz vale:
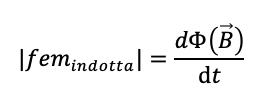
Il flusso del campo magnetico concatenato alla superficie del circuito in particolare vale
Φs (B) = B∙ S ∙ cosθ
in cui B è l'intensità del campo magnetico, S l'area della superficie attraversata dalle linee del campo ed θ l'angolo tra la normale alla superficie e le linee di campo. Poiché il campo è parallelo alla normale alla superficie allora cosθ = cos(0) = 1.
La superficie del circuito cambia istante per istante in quanto dipende dalla posizione della sbarretta. Essendo l'angolo a tra ipotenusa e cateto orizzontale di 45° vuol dire che il triangolo rettangolo che vediamo in figura è la metà di un quadrato il cui lato è proprio la distanza x dall'origine assunta dalla sbarretta.
Allora possiamo calcolare la superficie del circuito come:
S = x2 / 2
Il flusso allora vale:
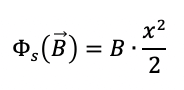
Ma possiamo riscrivere la posizione in funzione della velocità v della sbarretta come:
x = v ∙ t
e dunque:
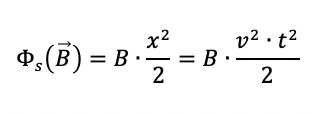
La fem indotta allora varrà:
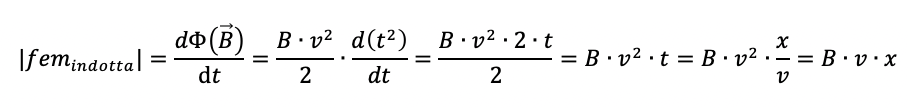
Allora la velocità espressa in funzione della posizione è :
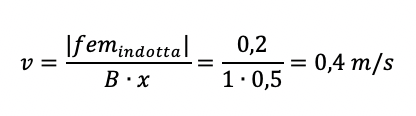
Per il calcolo della corrente indotta utilizziamo la prima legge di Ohm:
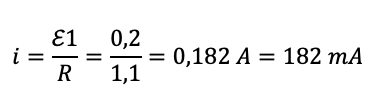
Link correlati:
Calcolo della coefficiente di autoinduzione di un solenoide
Esiste il monopolo magnetico?
Spiegazione dell'esperienza di Oersted
Studia con noi