Legge di Malus e fascio di luce polarizzata linearmente che attraversa due filtri polarizzatori
Esercizio sulla legge di Malus e fascio di luce polarizzata linearmente che attraversa due filtri polarizzatori
Un fascio di luce polarizzata linearmente attraversa due filtri polarizzatori. Il primo ha l'asse inclinato di un angolo a rispetto al piano di polarizzazione della luce incidente mentre il secondo ha un angolo di 90° rispetto alla luce incidente.
Determinare l'angolo a dell'asse del primo filtro affinché l'intensità finale del fascio trasmesso sia ⅒ di quello iniziale.
Svolgimento dell'esercizio

La legge di Malus afferma che l'intensità della luce trasmessa da un filtro polarizzazione in caso di polarizzazione incidente lineare è pari all'intensità dell'onda incidente I0 per il coseno al quadrato dell'angolo compreso tra la direzione di polarizzazione dell'onda incidente e la direzione di polarizzazione del polarizzatore:
Itrasmesso = I0 ∙ cos2α
Quando il fascio attraversa il primo filtro dunque l'intensità trasmessa sarà proprio pari a
I0 ∙ cos2α
Quando questo fascio attraversa il secondo filtro l'angolo tra questa direzione del fascio, che è la stessa di quella del primo filtro, e quella del filtro stesso è pari a 90 - α.
Per cui l'intensità trasmessa finale dopo il secondo filtro sarà:
Ifinale = I0 ∙ cos2α ∙ cos2(90-α)
Dalla trigonometria sappiamo che cos(90-α) = senα, per cui:
Ifinale = I0 ∙ cos2α ∙ sen2α
Imponendo che l'intensità finale del fascio sia ⅒ di quello iniziale otteniamo:
⅒ ∙ I0 = I0 ∙ cos2α ∙ sen2α
Da cui semplificando I0:
⅒ = cos2α ∙ sen2α
Ricordando che:
sen(2α) = 2 ∙ senα ∙ cosα (formula di duplicazione del seno) otteniamo:

Cioè:
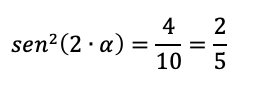
Da cui:

Oppure:

Ricordiamo che la soluzione di una equazione goniometrica del tipo
senx = α
è
x= arcsen(α)
e
x = 180° - arcsen(α)
Link correlati:
Esercizio svolto su lente sottile biconvessa
Esercizio sul calcolo del numero di fenditure di un reticolo di diffrazione
Esercizio svolto sul reticolo di diffrazione
Studia con noi