Prodotto scalare e prodotto vettoriale
Esercizio sul prodotto scalare e sul prodotto vettoriale
Siano 
e 
due vettori del piano di componenti rispettivamente:
= = (3;9)
= (4;5)
Determinare l'angolo compreso tra di essi, il prodotto scalare ed il prodotto vettoriale dei due vettori.
Svolgimento
La traccia del problema fornisce le componenti dei due vettori e .
La loro rappresentazione grafica su un sistema di assi coordinati è del tipo mostrata in figura.
Ogni vettore viene fatto partire dall'origine degli assi e forma un angolo con l'asse orizzontale.
Chiamati α e β i due angoli formati rispettivamente dai due vettori, l'angolo tra i due vettori è pari alla loro differenza.
Calcoliamo dunque i due angoli a partire dalle componenti:
= = (3;9)
= (4;5)
ax = 3
ay = 9
bx = 4
by = 5
L'angolo formato da un vettore con l'asse orizzontale è pari all'arcotangente del rapporto tra la componente verticale e quella orizzontale:
α = arctg(ay / ax ) = arctg (9/3) = arctg(3) = 71,6°
β = arctg (by/ bx ) = arctg (5/4) = arctg(1,25) = 51,4°
L'angolo θ compreso tra i due vettori vale dunque:
θ = α - β = 71,6° - 51,4° = 20,2°
Il prodotto scalare tra i due vettori è un valore scalare e rappresenta la proiezione del primo vettore sul secondo, in particolare esso vale:
= a · b · cos θ
in cui a e b sono i moduli dei vettori e .
In questo caso il prodotto scalare era calcolabile anche a partire della somma del prodotto delle componenti dei singoli vettori:
= = ax· bx + ay· by = 3·4 + 9·5 = 12 + 45 = 57
Il prodotto vettoriale restituisce ancora un vettore il cui modulo è dato da:
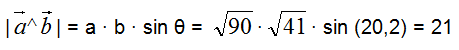
La direzione è quella perpendicolare al piano in cui sono poggiati i due vettori e mentre il verso stabilito mediante la "regola della mano destra" è entrante nel foglio.
In definitiva l'angolo compreso tra i due vettori vale 20,2°; il prodotto scalare dei due vettori è 57; il vettore risultante dal prodotto vettoriale ha modulo 21, direzione perpendicolare al piano in cui giacciono i due assi e verso entrante nel foglio.
Studia con noi