Esercizio su diagramma spazio tempo
Esercizio svolto e commentato su diagramma spazio tempo
Vi sono due gemelli di nome Mario e Giovanni.
Mario parte con la sua astronave dalla Terra mantenendo una velocità costante pari a ⅔∙c e rimane in viaggio 6,0 anni secondo la Terra.
Una volta passati i 6 anni, Mario rimane su di una stazione orbitale ferma rispetto alla Terra per 2 anni e riparte dunque indietro a velocità c/2.
Il suo gemello Giovanni nel frattempo è rimasto fermo a Terra.
Rappresentare in un diagramma spazio-tempo il viaggio di Mario e determinare quanto tempo è passato tra il viaggio di partenza e quello di ritorno di Mario sulla Terra.
Al suo ritorno quale sarà la differenza di età tra i due gemelli?
Svolgimento dell'esercizio
Fissiamo i tre eventi sul diagramma spazio tempo di Minkowski.
Innanzitutto l'evento O sarà il momento iniziale della partenza di Mario, ovvero il qui e ora per entrambi gli osservatori che si trovano in x= 0 m al tempo t = 0 s.
L'evento A sarà dato dal raggiungimento di Mario della stazione dopo 6 anni (tempo misurato dal gemello rimasto fermo a Terra); l'evento B sarà il momento in cui Mario torna verso la Terra ed infine il punto C sarà l'arrivo a casa.
Il punto O avrà ovviamente coordinate (0;0).
Il punto A avrà coordinata temporale pari a 6 anni mentre per il calcolo della coordinata spaziale consideriamo che Mario viaggia per 6 anni a velocità pari a ⅔∙c quindi:
xA = v ∙ Δt = ⅔ ∙c ∙ 6 = 4 anni luce
La retta OA avrà inclinazione maggiore alla bisettrice primo-terzo quadrante, rappresentando la linea di universo del viaggio di andata.
A(4;6)
Il punto B avrà coordinata spaziale uguale a A (Mario rimane fermo rispetto a Terra) ma saranno passati due anni, dunque la sua coordinata spaziale sarà pari a 6 + 2 = 8 anni
B (4; 8)
Il punto C sarà sull'asse c∙t in quanto Mario ritorna al punto x=0, avendo viaggiato a c/2 allora sarà passato un tempo rispetto alla Terra pari a:
Δt = 4 anni luce / (c/2) = 8 anni (che si sommano agli 8 anni già trascorsi).
La retta BC avrà coefficiente angolare negativo in quanto Mario si sta muovendo verso la direzione negativa dell'asse x tornando indietro. Cioè si starà muovendo a velocità -c/2 rispetto alla Terra. Allora le coordinate di C saranno:
C(0; 16)
Il diagramma sarà dunque (l'unità di misura dei due assi è l'anno luce):
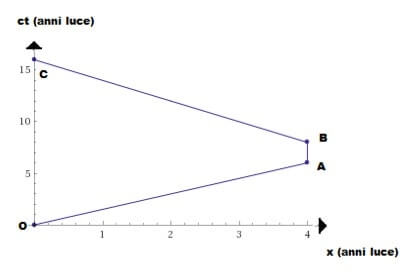
Dunque Mario ritorna sulla Terra dopo 16 anni dalla sua partenza (tempo misurato dal gemello rimasto fermo).
Durante il viaggio di andata (OA) tuttavia il tempo proprio percepito a bordo da Mario sappiamo per gli effetti relativistici essere inferiore a quello misurato da Giovanni e pari a 6 anni.
In particolare detti Δt' = 6 e Δt il tempo proprio avremo che:
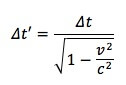
Il tempo proprio sarà allora pari a (v = ⅔ ∙ c):
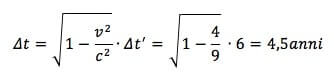
Dunque già Mario sarà più giovane di 1,5 anni rispetto ai 6 trascorsi per Giovanni.
Durante il viaggio di ritorno, durato per Giovanni 8 anni, per Mario saranno invece trascorsi (v = c/2):
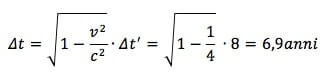
Dunque la differenza di età sarà adesso pari a 8 -6,9 = 1,1 anni. In totale Mario sarà più giovane rispetto a Giovanni di 2,6 anni.
Link correlati:
Esercizio svolto e commentato su effetto Doppler relativistico
Esercizio svolto e commentato sul diagramma di Minkowski
Esercizio svolto e commentato sull'esperimento di Michelson
Che cos'è l'effetto Doppler?
Studia con noi