Particella soggetta a due moti armonici semplici
Esercizio rigurdante una particella soggetta a due moti armonici semplici
Una particella è soggetta simultaneamente a due moti armonici semplici caratterizzati dalla stessa frequenza e dalla stessa direzione.
Le leggi orarie che regolano i due moti sono:
x1 = 10 ·sen(2·t)
e
x2 = 6 ·sen(2·t + 5· π/12)
Ricavare l'espressione del moto risultante.
Svolgimento
Siamo in presenza di due moti armonici simultanei regolati ognuno da una legge oraria fornita dal testo.
Notiamo anzitutto che la fase iniziale di x1 è zero mentre quella di x2 vale 5· π/12; per cui la differenza di fase tra i due moti risulta:
φ = 5· π/12
Il moto risultante a cui sarà soggetta la particella è:
x = x1 +x2 = 10 ·sen(2 · t) + 6 ·sen(2 · t + 5 · π/12)
ovvero la somma dei due moti.
Osserviamo il grafico sotto:

Sono stati riportati i due vettori rotanti di ampiezza A1 e A2 descritti dalle due leggi orarie.
Si vede che il vettore somma (in rosso) continuerà a girare ancora con la stessa velocità angolare e frequenza ma avrà ampiezza A data dal teorema di Carnot applicato al triangolo di lati A1, A2 ed A (immaginiamo di traslare nella figura sopra il lato A2 in modo da chiudere il triangolo con gli altri due lati), in cui conosciamo i due lati A1 e A2 e l'angolo tra loro compreso pari a φ.
Ricordiamo che per il teorema di Carnot:
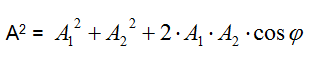
Quindi il moto risultante è sempre un moto armonico semplice con velocità angolare ω pari a:
ω = 2 rad/s
ma con ampiezza A pari a:
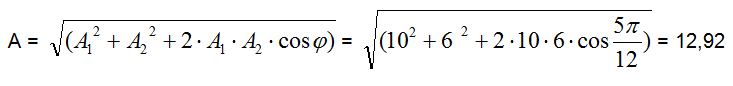
Per l'equazione che esprime x in funzione di t sarà del tipo:
x(t) = 12,92 · sen(2 · t + α)
con α differenza di fase tra x e x1.
Per ricavare α, notiamo che per t=0:
x(0) = 12,92 · senα
Ma poiché
x(0) = x1(0) +x2(0) = 10 · sen(2 · 0) + 6 ·sen(2 · 0 + 5 · π / 12) = 6 ·sen( 5 · π / 12) = 5,796
Ponendo a sistema le due precedenti:
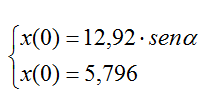
otteniamo
12,92 · sen α = 5,796
sen α = 5,796/12,92 = 0,4486
per cui
α = arcsen (0,4486) = 26,5° = 1,47 · π rad
In definitiva l'equazione oraria del moto composto dalla somma dei due moti originari sarà:
x(t) = 12,92 · sen(2 · t + 1,47 · π)
Link correlati:
Quali sono le formule del moto armonico?
Studia con noi