Corrente indotta e legge di Lenz
Calcolo della corrente indotta e applicazione della legge di Lenz
Su metà superficie di una spira a forma quadrata conduttrice di lato L = 2 m e resistenza R = 6,5 Ω agisce un campo magnetico B uniforme, perpendicolare alla spira e uscente dal foglio, come in figura.
Nel circuito è presente anche un generatore di forza elettromotrice fem = 3 V, di resistenza interna r = 0.5 Ω. Il modulo del campo magnetico decresce linearmente nel tempo e vale B0 = 0.5 T al tempo t0 = 0, per poi annullarsi in t1 = 0.25 s.
Calcolare, nell'intervallo di tempo Δt = t1 – t0:
a) l'intensità della corrente che scorre nella spira;
b) la carica che ha complessivamente attraversato la spira;
c) il lavoro compiuto dal generatore per far circolare la corrente.

Svolgimento
Poiché la spira è immersa per metà in un campo magnetico variabile avremo la generazione di una corrente indotta che ha come valore assoluto:
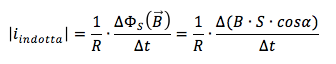
Possiamo usare il delta nella formula in quanto il campo sta variando linearmente (quindi la variazione coincide con la derivata).
In particola il coseno dell'angolo tra linee di campo magnetico e normale alla superficie vale 1 in quanto l'angolo tra di essi è zero (linee di campo uscenti dal foglio). Inoltre possiamo portare fuori dall'operazione di delta la superficie S che rimano costante:
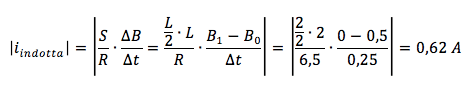
Poiché questa corrente indotta è generata da una diminuzione del flusso a causa della decrescita del campo B, essa genererà a sua volta un ulteriore campo magnetico con la proprietà di rafforzare quello esterno per la legge di Lenz.
Cioè il campo magnetico indotto avrà la stessa direzione e verso di quello esterno e quindi uscente dalla pagina. Per ottenere un campo con questo verso la corrente indotta nella spira deve circolare in senso antiorario (regola della mano destra).
La corrente i che scorre nel circuito a causa della presenza del generatore scorre dal polo + al polo – della batteria ideale quindi in senso antiorario.
Poiché ci sono due resistenze collegate in serie r ed R la corrente varrà:
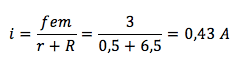
La corrente che circola in totale nel circuito è dunque la somma delle due correnti visto che entrambe circolano in senso antiorario:
itot = i + iindotta = 0,43 A + 0,62 A = 1,1 A
La carica che si avrà complessivamente attraversato la spira la si può dedurre dalla definizione di intensità di corrente elettrica:
i = ΔQ / Δt
Per cui la carica è il prodotto di i per l'intervallo di tempo:
ΔQ = i ∙ Δt = 1,1 ∙0,25 = 0,26 C
Il lavoro compiuto dal generatore per far circolare la corrente itot è pari al prodotto della potenza fornita per il tempo:
E = P ∙ Δt = fem ∙ itot ∙ Δt = 3 ∙ 1,1 ∙ 0,25 = 0,75 J
Link correlati:
Bobina che ruota in un campo magnetico uniforme e costante e calcolo dell'intensità del campo magnetico
Calcolo della costante di tempo di un circuito RC
Esercizio riguardante la scarica di un condensatore carico attraverso una resistenza
Studia con noi