Bobina che ruota in un campo magnetico uniforme e costante
Bobina che ruota in un campo magnetico uniforme e costante e calcolo dell'intensità del campo magnetico
La bobina di un alternatore è costituita da 150 spire circolari di raggio 5 cm. La bobina ruota con frequenza costante di 40 Hz in un campo magnetico uniforme e costante.
Sapendo che la massima f.e.m. indotta nella bobina è di 20 V, determina l'intensità del campo magnetico.
Svolgimento dell'esercizio
La bobina è in rotazione con frequenza f = 40 Hz all'interno di una regione dello spazio sede di un campo magnetico costante e uniforme che è l'incognita da ricavare. La fem indotta nella bobina composta da N spire in valore assoluto vale:

In cui
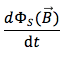
è la derivata del flusso del campo magnetico concatenato alla superficie del solenoide rispetto al tempo.
Ricordando l'espressione che ci permette di calcolare il flusso del campo magnetico è:
Φs (B) = B∙ S ∙ cosα
in cui B è l'intensità del campo magnetico, S la superficie di ogni spira che compone il solenoide e l'angolo α è quello tra le linee di campo magnetico e la normale alla superficie, possiamo riscrivere la fem indotta come:
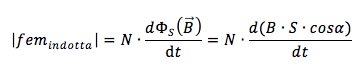
Essendo B e S costanti possono essere portati fuori dall'operatore di derivata:
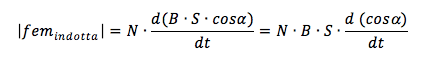
L'angolo a spazzato dalla rotazione della bobina sarà pari al prodotto della velocità angolare ω (espressa in rad/s) per il tempo t quindi
α = ω ∙ t
Allora la fem indotta vale:
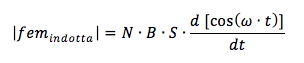
La pulsazione ω è però costante e vale
Ω = 2 ∙ π ∙ f
Dunque derivando il coseno di una funzione (ω∙t) rispetto al tempo otteniamo – seno della stessa funzione per la derivata dell'argomento rispetto a t. la derivata di ω∙t, essendo ω appunto costante, è ω. Allora:
![]()
in cui abbiamo tralasciato i segni.
La fem indotta sarà dunque una tensione variabile che varierà secondo una sinusoide. Sappiamo che il valore massimo che assume in valore assoluto è pari a 20 V e tale valore assoluto è dato dalle costanti moltiplicate alla funzione seno che come sappiamo può assumere solo valori compresi tra -1 e + 1. Dunque la fem max indotta sarà pari a:
![]()
Da qui possiamo ricavare il valore dell'intensità del campo magnetico B:
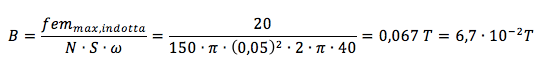
Link correlati:
Calcolo della costante di tempo di un circuito RC
Esercizio riguardante la scarica di un condensatore carico attraverso una resistenza
Studia con noi