Calcolo della frequenza di un pendolo
Esercizio sul calcolo della frequenza di un pendolo
Un pendolo semplice lungo 2 m è posto all'interno di un ascensore.
Calcolare la frequenza di oscillazione nei seguenti casi:
- l'ascensore è fermo
- l'ascensore sta salendo con un'accelerazione pari a 2 m/s2
- l'ascensore è in caduta libera
Svolgimento dell'esercizio
L'esercizio propone il caso di un pendolo lungo 2 metri che viene posto all'interno di un ascensore.
Si vuole determinare la frequenza di oscillazione del pendolo nelle tre condizioni citate nel testo dell'esercizio.
1° caso
Nel primo caso la frequenza di oscillazione è data semplicemente dal reciproco del periodo T calcolato come:

in cui:
- L è la lunghezza in metri del pendolo;
- g è l'accelerazione di gravità;
- T è il periodo del pendolo in secondi del pendolo.
Sostituendo i dati in nostro possesso si ha che:
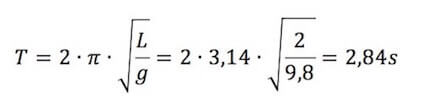
Da cui:
f = 1/T = 1/2,84 = 0,35 Hz
2° caso
Se l'ascensore sale con accelerazione a, il sistema non è più un sistema di riferimento inerziale ma sul pendolo agirà un'accelerazione relativa pari alla somma dell'accelerazione di gravità g più l'accelerazione a dell'ascensore per cui il periodo sarà pari a:
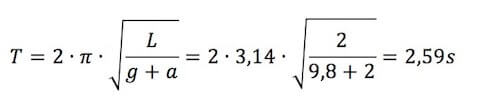
Da cui:
f=1/T = 1/2,59= 0,39 Hz
3° caso
Infine nell'ultimo caso di ascensore in caduta libera ogni corpo all'interno di esso e quindi anche il pendolo sentiranno un'accelerazione relativa pari alla differenza tra l'accelerazione di gravità e l'accelerazione con cui scende l'ascensore.
Per cui l'accelerazione relativa è nulla per il pendolo.
Poiché l'accelerazione rappresenta il denominatore del rapporto cui dipende il periodo, questo vuol dire da un punto di vista matematico che il periodo del pendolo diventa infinito e corrisponde ad una sua frequenza nulla.
In termini più fisici il pendolo rimane fermo e non oscilla.
Link correlati:
Che cos'è il periodo di un pendolo?
Che cosa sono il periodo e la frequenza di un pendolo?
Che cos'è l'isocronismo del pendolo?
Studia con noi