Trasformazione stella triangolo
Come avviene la trasformazione stella triangolo?
Le trasformazioni stella triangolo sono utilizzate per risolvere circuiti in cui le resistenze sono posizionate in maniera tale da non risultare né in serie né in parallelo tra di loro.
Consideriamo ad esempio questo circuito:

Le resistenze 2, 4, 5, 6 e 7 non sono poste né in serie né in parallelo tra di loro e quindi per risolvere il circuito si può far ricorso alla trasformazione stella triangolo. In particolare la maglia ABC si può ridisegnare in maniera equivalente come un triangolo:

in cui sono presenti i nodi A, B e C che rappresentano i vertici del triangolo mentre i lati sono rappresentati dalle resistenze 2,5 e 6. Analogamente la maglia CBD si può ridisegnare come un altro triangolo:

Quindi i resistori 4, 5 e 7 avranno una configurazione a triangolo con i vertici rappresentati dai nodi B, C e D.
Nel circuito di cui ci stiamo occupando è possibile anche estrapolare delle configurazioni a stella, in particolare le resistenze 5, 6 e 7 possono essere disegnate in una configurazione detta a stella:

La stella è caratterizzata da un centro stella, il nodo C, e dai tre terminali A, B e D. L'altra configurazione a stella riguarda invece le resistenze 2, 4 e 5:
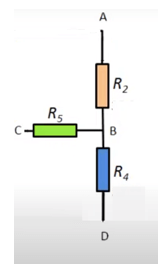
con centro stella il nodo B e punte con i nodi A, C e D.
Equivalenza elettrica stella triangolo
Per trasformare una configurazione a triangolo in una a stella o viceversa è necessario che le due configurazioni siano equivalenti da un punto di vista elettrico. L'equivalenza elettrica tra le due configurazioni si ha quando sostituendo una stella con un triangolo o viceversa tutte le correnti e le tensioni che non fanno parte della stella o del triangolo rimangono invariate.
Consideriamo ad esempio la configurazione stella o triangolo ABC, nel caso di stella ABC saranno le punte della stella mentre nel caso del triangolo saranno i vertici. Se vogliamo che le due configurazioni caratterizzate dagli stessi nodi siano equivalenti dobbiamo imporre che le resistenze tra ogni nodo di entrambe le configurazioni siano uguali:
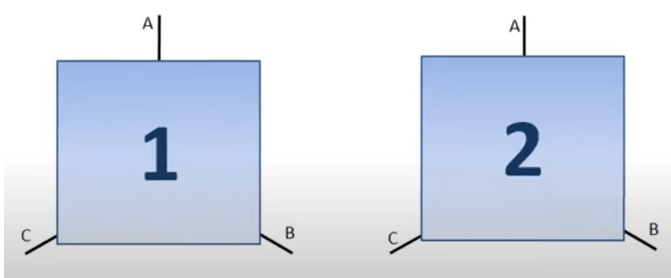
Quindi dovrà essere che RAB1 = RAB2, RBC1 = RBC2 e RCA1 = RCA2.
Consideriamo allora un triangolo ed una stella caratterizzati dagli stessi nodi e calcoliamone le varie resistenze tra i nodi. Chiamiamo RAB, RBC e RCA le resistenze del triangolo e RA, RB e RC quelle della stella.

Per il triangolo quando andiamo a calcolare la resistenza tra il nodo A e B è come se disattivassimo il nodo C che è lasciato libero e dunque non rappresenta più elettricamente un nodo. Quindi le resistenze RCA e RBC sono collegate in serie tra di loro e la loro serie è in parallelo con RAB. Questo discorso vale quindi anche quando consideriamo al resistenza tra i nodi B e C. A non rappresenterà più un nodo e quindi la resistenza RBC sarà in parallelo con la serie tra RCA e RAB.
Ricordando che la resistenza equivalente di due resistenze poste in serie è pari alla somma delle due e che il parallelo tra due resistenze è equivalente ad una resistenza con resistenza equivalente pari al prodotto delle due diviso la somma otteniamo che le tre resistenze tra i nodi del triangolo valgono:

Consideriamo adesso la stella. Quando vogliamo calcolare la resistenza tra i nodi A e B il nodo C è libero e quindi risulterà che le resistenze RA e RB sono in serie per cui risulta che la loro resistenza equivalente varrà RAB2 = RA + RB.
Allo stesso modo saranno poste in serie le resistenze B e C quando considero i due nodi B e C. Per cui alla fine avremo che:

In definitiva avremo:

Per avere l'equivalenza delle due configurazioni, tutte le resistenze tra i nodi devono essere uguali. Per cui deve risultare:
RAB1 = RAB2, RBC1 = RBC2 e RCA1 = RCA2
Ovvero avremo le seguenti uguaglianze:
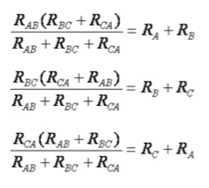
Risolvendo il sistema si possono ricavare le espressioni che restituiscono le tre resistenze del triangolo in funzione di quelle della stella e viceversa:

Analizzando queste formule si può osservare che la resistenza di ciascun lato del triangolo è uguale al rapporto tra uno stesso numeratore, formato dalla somma dei prodotti delle tre resistenze della stella prese a due a due, e la resistenza che fa capo al vertice opposto al alto di cui sto cercando la resistenza (nel primo caso ci sarà RC a denominatore in quanto sto cercando la RAB).
La resistenza che fa invece riferimento ad ogni punta della stella è data dal rapporto tra un numeratore dato dal prodotto delle due resistenze del triangolo che fanno capo allo stesso vertice divido la somma delle tre resistenze del triangolo (nel primo caso a numerato ci sarà il prodotto RAB ∙ RCA in quanto entrambe fanno capo allo stesso vertice A).
Link correlati:
Esercizio svolto sulla trasformazione stella triangolo
Elenco delle formule per la trasformazione stella triangolo
Come si risolve un circuito elettrico?
Comportamento di diversi circuiti in regime sinusoidale
Studia con noi