Teorema di Torricelli
Spiegazione del teorema di Torricelli
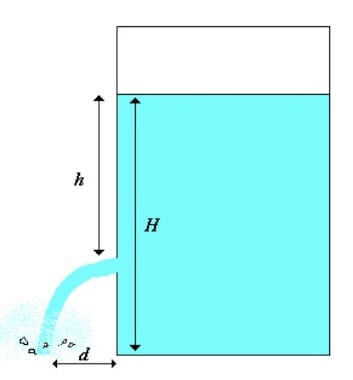
Consideriamo un recipiente riempito di un liquido fino a una certa altezza h a partire da un piccolo foro praticato sulla sua superficie laterale.
Se la sezione del contenitore è molto grande rispetto a quella del foro, possiamo praticamente considerare prossima allo zero la velocità con cui si muove il liquido sulla superficie libera:
Applichiamo l'equazione di Bernoulli:
P + ρ ∙ g ∙ h + ½ ∙ ρ ∙ v2 = costante
alla situazione appena descritta:
P1 + ρ ∙ g ∙ h1 + ½ ∙ ρ ∙ v12 = P2 + ρ ∙ g ∙ h2 + ½ ∙ ρ ∙ v22
Sulla superficie libera i valori di pressione, velocità e quota saranno:
P1 = Patmosferica ; quota = h; v1 ≈0
Mentre le stesse grandezze misurate sul foro valgono:
P2 = Patmosferica ; quota = 0; v2 ≈v
Per cui otteniamo:
Patm + ρ ∙ g ∙ h = Patm + ½ ∙ ρ ∙ v2
Semplifichiamo Patm e ρ:
g ∙ h = ½ ∙ v2
Da cui:

che rappresenta il teorema di Torricelli ed afferma che la velocità di deflusso di un liquido da un piccolo foro laterale praticato sul contenitore posto ad una distanza h dal pelo libero è uguale alla velocità che lo stesso avrebbe se cadesse in moto di caduta libera dalla stessa altezza h.
Esercizio #1
In un grande serbatoio è contenuta dell'acqua fino ad un'altezza di 8 metri.
Viene praticato un foro 2 metri sotto al livello dell'acqua e ne fuoriesce un getto che arriva a colpire il piano orizzontale ad una certa distanza d dal serbatoio stesso.
Calcolare tale distanza.
Lo svolgimento dell'esercizio lo trovi qui: esercizio sul teorema di Torricelli.
Esercizio #2
Un serbatoio per l'acqua si trova alla sommità di un edificio ed è riempito tale che il livello superiore arriva a 30 m dal suolo.
Attraverso il serbatoio partono le tubature che portano acqua ai vari appartamenti dell'edificio e tali tubature hanno una sezione molto inferiore alla sezione del serbatoio.

Ogni appartamento è dotato di rubinetteria provvista di orifizi da cui esce l'acqua con sezione di 10 cm2 (centimetri quadrati).
Calcolare quanto tempo occorre per riempire un contenitore di capacità 30 dm3 posto in un appartamento che si trova a 20 m dal suolo.
Lo svolgimento dell'esercizio lo trovi qui: velocità di fuoriuscita dell'acqua da un rubinetto.
Link correlati:
Che cos'è la foronomia?
Studia con noi