Pompe con portate diverse
Esercizio su due pompe con portate diverse
Per riempire una piscina si utilizzano due diverse pompe che hanno una diversa portata.
La seconda pompa impiegherebbe 2 ore di tempo in più rispetto alla prima se dovesse riempire da sola la piscina.
Mentre se usate contemporaneamente le due pompe impiegano un tempo totale di 1 ora e 20 minuti.
Quanto tempo impiegherebbero le due pompe se dovessero separatamente riempire la piscina?
Svolgimento dell'esercizio
Chiamiamo Q1 e Q2 le portate delle due pompe.
Sappiamo che la portata Q è definita come rapporto tra volume e tempo:
Q = volume / tempo
Pertanto il volume totale di acqua che passa dalla prima pompa può essere espresso come prodotto della sua portata costante per il tempo totale di riempimento della vasca.
Chiamato t il tempo che impiega la pompa avremo:
V = Q1 ∙ t
Analogamente la seconda pompa impiega un tempo pari a (t + 2) h per riempire la vasca di un volume V:
V = Q2 ∙ (t + 2)
Uguagliando le due espressione otteniamo la condizione:
Q1 ∙ t = Q2 ∙ (t +2)
Quando le due pompe lavorano contemporaneamente allora si somma la portata delle due come è intuitivo pensare per cui lo stesso volume sarà pari al prodotto della somma delle portate per 1h e 20 m:
t = 1 h e 20 m = 1 + (20/60) = 80/60 = 4/3 h
V = (Q1 + Q2) ∙ 4/3
Ricaviamo Q1 dalla precedente:
Q1 = (¾) ∙ V - Q2
Sostituiamo in:
Q1 ∙ t = Q2 ∙ (t +2)
ed otteniamo:
[(¾) ∙ V - Q2] ∙ t = Q2 ∙ (t +2)
Ma:
V = Q2 ∙ (t +2)
Dunque:

Possiamo raccogliere e semplificare il termine Q2 in quanto compare in ambo i membri:
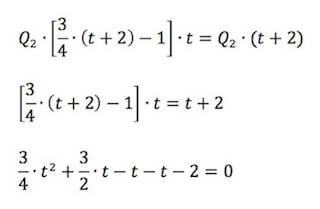
Moltiplicando per 4 tutti i termini e sommando si ha che:
3 t2 - 2t - 8 = 0
Le due soluzioni saranno:
t1 = -4/3
e
t2 =2
Scartando la soluzione negativa priva di significato fisico, la risposta dunque è 2 h.
Ovvero la prima pompa impiegherà un tempo pari a 2 h mentre la seconda un tempo superiore di 2 h ovvero 2 +2 = 4 h.
Link correlati:
Esercizio sul calcolo della prevalenza di una pompa
Studia con noi