Fascio di protoni che deve essere curvato di 90°
Esercizio su un fascio di protoni che deve essere curvato di 90°
Un fascio verticale di protoni deve essere curvato di 90° per diventare orizzontale in una lunghezza pari a 1,5 m.
Il fascio viene così accelerato da una ddp pari a 7MV ed immesso in una regione di spazio sede di un campo magnetico uniforme.
Determinare l'intensità del campo magnetico necessario ad effettuare tale operazione. (Si sappia che la massa del protone è pari a 1,67∙10-27 kg).

Svolgimento dell'esercizio
Calcoliamo innanzitutto la velocità con cui ogni singolo protone arriva nella regione di spazio sede del campo magnetico.
I protoni come si legge dal testo del problema sono accelerati da una ddp pari a 7 MV partendo da fermi, quindi acquisiscono un'energia cinetica pari al lavoro pari al prodotto della carica del protone per la ddp:
L = Ek = q∙ΔV = 1,6 ∙ 10-19 ∙ 7 ∙ 106 = 11,2 ∙ 10-13 J
Ricordando che l'energia cinetica è pari a:
EK = ½ ∙ m ∙ v2
La velocità raggiunta da ogni singolo protone sarà uguale a:

Poiché i protoni penetrano nel campo magnetico con una velocità che ha direzione perpendicolare al campo stesso, allora si muoveranno di moto circolare uniforme.
La lunghezza L rappresenterà proprio il raggio della circonferenza della traiettoria del fascio di protoni. Tale raggio vale:

Allora il campo B avrà intensità pari a:
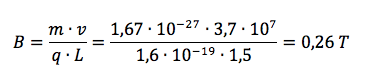
Pertanto l'intensità del campo magnetico necessaria per curvare di 90 il fascio di protoni è pari a 0,26 tesla.
Link correlati:
Esercizio sul moto di un protone in un campo magnetico
Calcolo della coefficiente di autoinduzione di un solenoide
Esercizio sul calcolo del numero di spire e lunghezza di un solenoide
Spiegazione dell'esperienza di Oersted
Studia con noi