Dimostrare che un triangolo è isoscele

Date le coordinate dei tre vertici, dimostrare che un triangolo è isoscele

I tre vertici di un triangolo ABC hanno coordinate A (-2;-3), B (-1;2) e C (4;1).

Dimostrare, attraverso l'utilizzo dei vettori del piano, che il triangolo in questione è isoscele.

Svolgimento

Il problema fornisce le tre coordinate dei vertici di un triangolo riferiti ad un piano xy e chiede si verificare se il triangolo è isoscele.

Ricordiamo che un triangolo è isoscele se due lati sono congruenti.

Trattiamo ogni lato del triangolo come un vettore che chiameremo: , e .

Le componenti x ed y di ogni vettore, ovvero le loro proiezioni sugli assi coordinati sono:

= = (-1 - (- 2) ; 2 - (-3) ) = (1, 5)

= = (4 - (-1) ; 1 -2) = (5, -1)

= = (4 - (-2); 1 - (-3) ) = (6, 4)

Calcoliamo adesso il modulo di ogni vettore, che corrisponde alla lunghezza di ogni lato del triangolo:

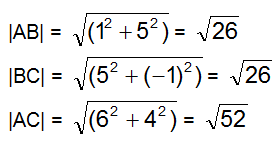
Poiché i vettori e hanno il medesimo modulo, pari a , il triangolo è allora isoscele.

Studia con noi