Vettore spostamento risultante
Calcolo del vettore spostamento risultante
Un aereo percorre 100 km in direzione nord, per poi virare e percorrere 150 km in direzione nord 30° est ed infine percorre 300 km in direzione est.
Calcolare lo spostamento risultante in modulo, direzione e verso.
Svolgimento
Il testo del problema fa riferimento a tre spostamenti relativi ad un aereo che sta volendo.
Lo spostamento è una grandezza vettoriale, infatti il vettore spostamento è dotato di modulo (quanto vale lo spazio percorso), direzione e verso.
In particolare i moduli dei tre vettori sono i seguenti:
S1 = 100 km
S2 = 150 km
S3 = 300 km
Proviamo a rappresentare graficamente i tre vettori e a tracciarne graficamente la risultante:
Come si può notare il primo vettore spostamento 
è diretto verso nord ovvero verticalmente verso l'alto; il secondo vettore 
è invece inclinato di 30° rispetto alla direzione verticale (nord) verso est (ovvero verso destra) ed infine il terzo vettore 
è diretto verso est quindi orizzontalmente verso destra.
Scriviamo le componenti di ogni vettore:
S1x =0
S1y = S1 = 100 km
Il vettore ha solo componente verticale essendo posizionato proprio verticalmente.
S2x = S2 · cos60 = 150 · cos60 = 75 Km
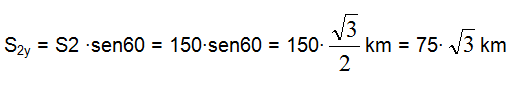
Infatti l'angolo tra il vettore e la direzione orizzontale è dato dalla differenza di un angolo retto meno i 30° che separano il vettore dalla direzione verticale.
Sarebbe stato anche corretto ed avremmo ottenuto lo stesso risultato scrivendo:
S2x = S2 ·sen30
S2y = S2 ·cos30
Dipende su quale triangolo rettangolo applichiamo le regole della trigonometria.
In generale è però preferibile sempre la prima scrittura.
Infine il vettore ha componenti:
S3x = 300 km
S3y = 0
Il vettore ha solo componente orizzontale essendo posizionato proprio orizzontalmente.
Detto 
il vettore spostamento risultante, quest'ultimo avrà componenti x ed y pari alla somma di ogni componenti di ciascun vettore:
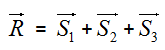
Quindi ad un'una equazione vettoriale corrispondono due equazioni scalari con cui possiamo calcolare le componenti del vettore .
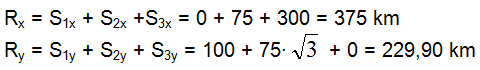
La risultante avrà dunque modulo pari a:
Infine per calcolare direzione e verso della risultante, detto α l'angolo che essa forma con l'asse orizzontale, sappiamo che:
R·cos α = Rx
R·sen α = Ry
Dividendo membro a membro le due suddette uguaglianze otteniamo:
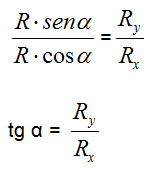
ed infine:
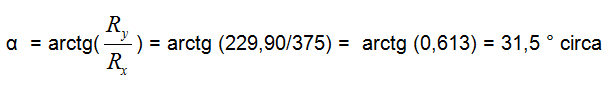
Quindi il vettore spostamento risultante è pari in modulo a 439,86 km ed ha direzione Est 31,5° Nord ( oppure Nord 58,5° Est).
Studia con noi