Esercizio su urto elastico
Esercizio svolto su urto elastico di una pallina contro una parete
Stabilire cosa succede quando un corpo di massa m, lanciato a velocità V colpisce una parete di massa M, con M molto maggiore di m.
Supporre urti elastici e frontali.
Svolgimento dell'esercizio
Il corpo di massa m sta viaggiando a velocità V contro una parete di massa M, la cui massa può essere considerata molto maggiore di quella del corpo in movimento.
In base a questa considerazione, possiamo scrivere che il rapporto delle due masse tende a zero, ovvero:
m/M ≈ 0
Le due velocità finali, del corpo e della parete, dopo l'urto sono date da:

e

Iniziamo col considerare il corpo 1, quello in movimento.
Innanzitutto possiamo affermare con certezza che la parete è fissa per cui la sua velocità iniziale è nulla
V2i = 0
Per cui:
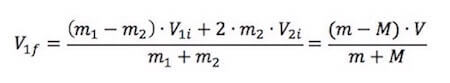
Raccogliamo M sia a numeratore sia a denominatore:
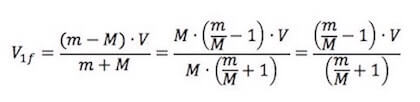
Ma per la considerazione iniziale sulle masse:
m/M ≈ 0
si ha che:

Per la parete invece:

Raccogliamo anche in questo caso M sia al numeratore che al denominatore:

Essendo:
m/M ≈ 0
Il numeratore si annulla e dunque:
V2f ≈ 0
Dunque, la pallina torna indietro dopo l'urto elastico con la parete con la stessa velocità in modulo e direzione ma con verso contrario (-V) mentre la parete rimane ferma come già ragionevolmente si era convenuti.
Studia con noi