Esercizio su circuito puramente induttivo
Esercizio svolto su circuito puramente induttivo
Un'induttanza L=12,7 mH è collegata ad un generatore di tensione alternata che eroga un ddp variabile nel tempo secondo la legge:
V(t) = V0 ∙ sen(ω∙t)
in cui V0 = 25 V
e
ω = 377 rad/s.
Calcolare il massimo valore della corrente e il valore della tensione quando la corrente è massima.
Svolgimento dell'esercizio

In un circuito puramente induttivo, cioè in cui è presente solo l'induttanza, la reattanza induttiva Z è pari alla pulsazione ω della fem per il valore dell'induttanza L:
Z = XL = ω ∙L
Inoltre sappiamo che la corrente oscilla in ritardo di un quarto di periodo, cioè π/2 (un periodo completo per le funzioni seno e coseno vale 2π) rispetto alla fem:

Il problema chiede di calcolare la tensione al tempo t* in cui la corrente è massima.
La corrente è massima in valore assoluto quando vale:
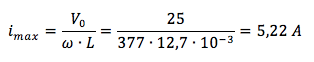
Ci chiediamo ora a quale istante di tempo t* la corrente assume tale valore?
Questo vuol dire risolvere l'equazione in cui il seno è uguale a 1 (perché una funzione sinusoidale assume il massimo quando il seno è +1 o -1); quindi:

Questo è il primo istante di tempo in cui la corrente assume il suo valore massimo, ovviamente essendo la funzione periodica continuerà ad oscillare infinite volte e assumerà infinite volte tale valore (in modulo) per ogni t* a cui aggiungiamo un angolo di π.
Calcoliamo allora la tensione all'istante t*:
V(t*) = V0 ∙ sen(ω∙t*) = 25∙ sen(π) = 0 V
In effetti essendo le due funzioni sfasate di π/2 quando la corrente è massima la tensione è zero.
Link correlati:
Esercizio svolto e commentato su circuito RLC
Comportamento di diversi circuiti in regime sinusoidale
Che cos'è un trasformatore ideale?
Che cos'è un circuito RLC?
Esercizio svolto su trasformatore
Esercizi online e gratuiti sulla prima legge di Ohm
Che cos'è la corrente alternata?
Studia con noi