Moto parabolico obliquo con spazio iniziale non nullo lungo y
Esercizio moto parabolico obliquo con spazio iniziale non nullo lungo la verticale
Un palla viene lanciata dalla cima di un palazzo alto 32 m con un angolo di inclinazione di 30° rispetto all'orizzontale.
Se la velocità con cui viene lanciata è di 10 m/s determinare l'altezza massima raggiunta, il tempo in cui sta in volo, la distanza orizzontale dal palazzo in cui essa atterra, la velocità con cui giunge al suolo.
Svolgimento
Si tratta di un moto parabolico obliquo con spazio iniziale non nullo lungo y.
Scegliendo un opportuno sistema di riferimento:

Scriviamo le equazioni del moto sapendo che:
Ho = + 32 m
α = 30°
Vo = 10 m/s
Detti Vo il modulo della velocità iniziale ed α l'angolo che essa forma con l'asse x, le due leggi orarie saranno del tipo:
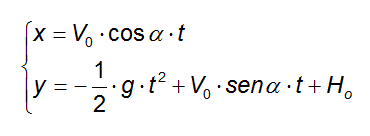
In cui (Vo · cosα) e (Vo · senα) sono rispettivamente le componenti orizzontali e verticali della velocità.
Ricaviamo t dalla prima equazione
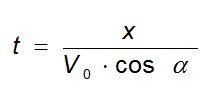
e sostituiamo nella seconda:
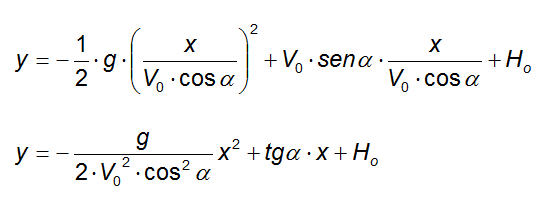
Questa rappresenta l'equazione cartesiana della traiettoria con cui si muove il corpo.
Ora l'altezza massima raggiunta corrisponderà alla coordinata y del vertice della parabola, che ricordiamo essere pari a:
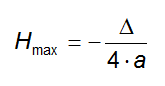
Ricaviamo i coefficienti a, b e c della parabola così da poter agevolmente procedere ai conti:
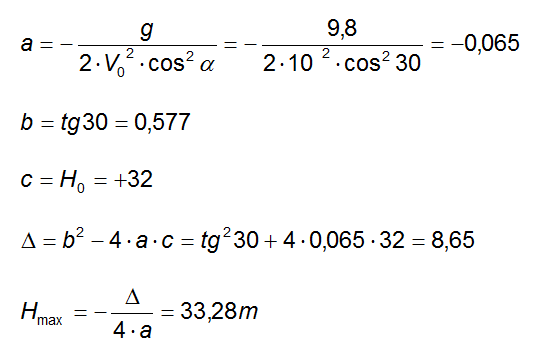
Per calcolare il tempo in cui sta in volo imponiamo che y = 0 nell'equazione della traiettoria, imponiamo cioè che la coordinata verticale sia nulla: questo accade quando la palla tocca il suolo.
Le due soluzioni saranno pari a:
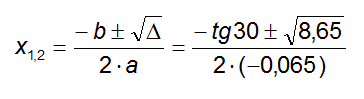
Scartiamo la soluzione negativa, in quanto priva di significato fisico, ed otteniamo:
x = 27,06 m che rappresenta la gittata.
Il tempo di volo, poiché il corpo si è mosso di moto rettilineo uniforme lungo l'asse x, sarà pari a:
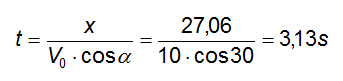
Dobbiamo infine calcolare la velocità con cui giunge al suolo. Le due componenti orizzontale e verticale della velocità variano come segue:
Vx = Vox
Vy = - g t + Voy
Per cui al tempo t = 3,13 s (tempo di atterraggio) avremo:
Vx = Vo · cosα = 10 · cos30 = 8,6 m/s
Vy = - g t + Voy = - 9,8 · 3,13 + 10 · sen30 = -25,67 m/s
Per cui il modulo della velocità risulterà pari alla radice quadrata della somma dei quadrati:
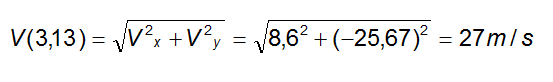
In definitiva:
l'altezza massima raggiunta vale 33,28 m, il tempo in cui sta in volo 3,13 s, la distanza orizzontale dal palazzo in cui essa atterra è 27,06 m, la velocità con cui giunge al suolo 27 m/s.
Link correlati:
Quali sono le formule sul moto parabolico?
Studia con noi