Relazione tra un moto parabolico ed un moto rettilineo uniformemente accelerato
Esercizio sul calcolo delle coordinate x e y del punto di incontro tra due corpi aventi due moti diversi
Una pallina viene lasciata cadere dal punto di coordinate (3 m ; 2 m) e contemporaneamente un'altra pallina viene lanciata dall'origine con il vettore velocità diretto come la congiungente tra l'origine e il punto in cui è presente l'altro corpo.
Il modulo della velocità vale 8 m/s.
Quali saranno le coordinate x e y del punto di incontro tra i due corpi?
Svolgimento
Il problema pone in relazione un moto di tipo parabolico (pallina che viene lanciata dall'origine) ad un moto rettilineo uniformemente accelerato (pallina che cade):

Le due traiettorie nel piano, parabola e retta, si intersecheranno in un punto che rappresenta il punto di incontro tra le due palline.
Calcoliamo anzitutto l'inclinazione α della velocità iniziale.
Dal testo si evince che la velocità ha la stessa direzione della congiungente tra l'origine e il punto di coordinate (3;2), pertanto l'angolo sarà:
tg α = ⅔
da cui
α = arctg ⅔ = 33,5 ° circa.
Scriviamo adesso le due leggi orarie che descrivono il moto nelle due direzioni x e y per la pallina che si muoverà di moto parabolico:

Con
Vox = Vo · cos α
e
Voy = Vo · sen α
Ricaviamo t dalla prima equazione
t = X / V0x
e sostituiamo nella seconda:
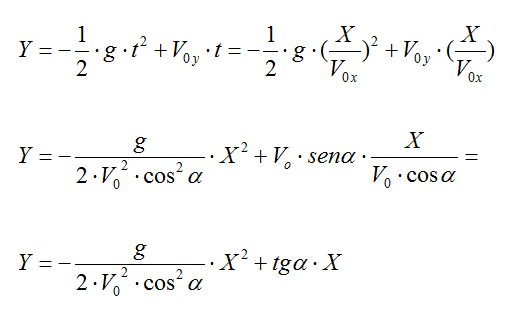
Ora poiché la pallina in caduta libera si muoverà lungo la retta verticale di equazione X = 3 imponiamo questo valore della X nell'equazione della parabola che abbiamo appena ricavato e calcoliamo la quota Y a cui avviene l'incontro:

Pertanto le due palline si incontreranno nel punto di coordinate (3;1).
Link correlati:
Quali sono le formule sul moto parabolico?
Studia con noi