Cariche elettriche poste nel vuoto
Esercizio su cariche elettriche poste nel vuoto
Due sferette possiedono entrambe carica positiva, tali per cui la somma di queste cariche è pari a 5,0·10-5 C.
Una volta poste nel vuoto a 2,0 metri di distanza l'una dall'altra, queste di respingono con una forza di intensità pari a 1 N.
Calcolare il valore di ciascuna delle due cariche.
Svolgimento
Scriviamo in ordine i dati forniti dal problema:
Q1 + Q2 = 5,0·10-5 C
r = 2,0 m
|F| = 1 N
Tra le due cariche si instaura una forza elettrica di tipo repulsivo, in quanto esse possiedono ciascuna una carica di segno positivo.
La legge di Coulomb, che descrive tale forza di interazione a distanza che si instaura tra le cariche elettriche, ha la seguente espressione:

in cui
K0 è detta costante di Coulomb e vale nel vuoto 9·109 N·m2/C2
r è la distanza tra le due cariche.
Sapendo che il modulo della forza è 1 N possiamo allora scrivere:
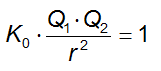
Da cui:
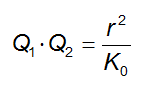
Sapendo dai dati inoltre che
Q1 + Q2 = 5,0·10-5 C
possiamo porre a sistema le due equazioni:
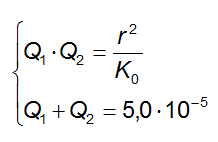
Sostituendo i valori numerici:
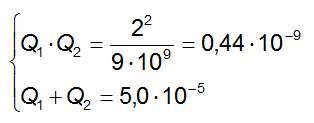
Il sistema appena scritto è composto da due equazioni in due incognite Q1 e Q2 e può essere facilmente risolvibile tramite il metodo di sostituzione.
Ricaviamo una delle due incognite dalla seconda e sostituiamo nella prima:
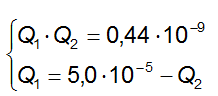
Ovvero:
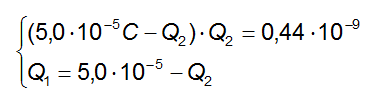
Procediamo alla risoluzione della prima equazione:
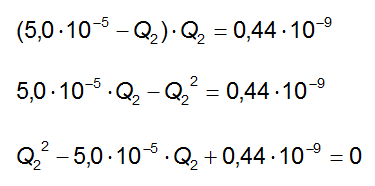
Quest'ultima rappresenta un'equazione di secondo grado in Q2:
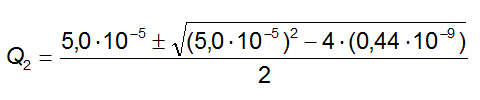
otteniamo:
Q2 = 3,84·10-5 C
e
Q2 = 1,16·10-5 C
Ora considerando che
Q1 + Q2 = 5,0·10-5 C
Otteniamo che*
Q1 = 5,0·10-5 - Q2
Quindi in definitiva otteniamo che la coppia di sfere ha cariche pari a:
Q1 = 1,16·10-5 C
Q2 = 3,84·10-5 C
*Questo perché i due valori di Q2 derivavano dalla risoluzione di un'equazione di secondo grado, e comunque vengano scelti, anche cambiando i pedici, i valori vengono sempre 3,84 ·10-5 C e 1,16 ·10-5 C.
Poiché le cariche infatti interagiscono tra di loro è la medesima cosa scambiare le due cariche cioè la 1 con la 2 o viceversa ai fini della soluzione dell esercizio.
Studia con noi