Esercizio sul venturimetro
Esercizio su un venturimetro posto in orizzontale
Un venturimetro (tubo di Venturi) è un dispositivo costituito da un tubo orizzontale in cui è presente una strozzatura centrale che serve a calcolare la velocità con cui scorre un fluido al suo interno:

Nei due punti indicati in figura, ovvero prima della strozzatura e lungo la strozzatura, sono posizionati due manometri che misurano la pressione del fluido.
Calcolare in funzione della differenza di pressione, della densità del fluido e delle caratteristiche fisiche del condotto, la velocità con cui scorre il fluido.
Svolgimento
Chiamiamo rispettivamente con 1 e 2 i due punti all'interno del venturimetro, ovvero i punti rispettivamente in cui la sezione del tubo è normale A1 e quello invece in cui è presente la strozzatura A2.
Nell'ipotesi di fluido ideale, ovvero incomprimibile, vale l'equazione di continuità:
Q = S · v = costante
in cui
- Q è la portata del fluido;
- S è la superficie del condotto attraversata dal fluido;
- v la velocità.
Per cui possiamo scrivere per i due punti in considerazione che:
A1 · V1 = A2 · V2
Esprimiamo dunque V2 come:

Secondo il teorema di Bernoulli, nel venturimetro in cui scorre il fluido di densità ρ presi i due punti 1 e 2 in cui il fluido scorre rispettivamente con velocità V1 e V2, una volta misurate le pressioni P1 e P2 tramite i due manometri e considerando h1 e h2 le quote dei due punti rispetto ad un riferimento orizzontale, uguali in questo caso in quanto il tubo è orizzontale, vale la seguente equazione:
P1 + ρ · g · h1 + ½ · ρ · V12 = P2 + ρ · g · h2 + ½ · ρ · V22
Dividendo entrambi i membri per ρ · g otteniamo:

Per cui:
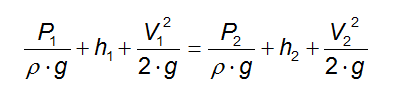
Essendo come già detto la conduttura posta in orizzontale:
h1 = h2
dunque possiamo semplificare entrambe le quote h in tutti e due i membri ed otteniamo:

Possiamo semplificare g:

Sostituiamo in questa espressione quella precedentemente ricavata per la velocità al punto 2:

Moltiplichiamo entrambi i membri per 2·ρ:

Raccogliamo V12:

Da cui:

Studia con noi