Elettrone lanciato all'interno di un condensatore con una angolazione di 45°
Studio del moto di un elettrone lanciato all'interno di un condensatore con una angolazione di 45°
Un elettrone è lanciato all'interno di un condensatore in cui è presente un campo elettrico E = 2,0 · 103 N/C con una velocità pari a 6,0 · 106 m/s, ed una direzione inclinata di 45° rispetto all'orizzontale:

Sapendo che le due armature distano 2,0 cm e sono lunghe 10,0 cm stabilire se l'elettrone urterà una tra le due armature ed in caso affermativo dire dove.
Svolgimento
I dati a disposizione sono i seguenti:
e = -1,6 · 10-19 C (carica di un elettrone)
m = 9,1 · 10-31 kg (massa di un elettrone)
E = 2,0 · 103 N/C
Vo = 6,0 · 106 m/s
α = 45°
d = 2,0 cm
L = 10,0 cm
L'elettrone, che è una particella dotata di carica negativa, viene introdotto all'interno di un condensatore in cui è presente un campo elettrico E diretto verso l'alto.
Ricordando la definizione di campo, l'elettrone sentirà una forza pari a ![]() in cui q è la carica dell'elettrone.
in cui q è la carica dell'elettrone.
La carica di un elettrone è pari a:
e = -1,6 · 10-19 C
Per cui la forza di cui risentirà l'elettrone sarà di verso opposto a quello del campo che quindi tenderà a frenare l'elettrone decelerandolo con un'accelerazione pari a:
a = F/m
diretta verso il basso e presente quindi solo sull'asse y.
Sull'asse x invece l'elettrone si muoverà di moto rettilineo uniforme; sull'asse y di moto rettilineo uniformemente accelerato.
La composizione dei due moti sarà una moto parabolico:
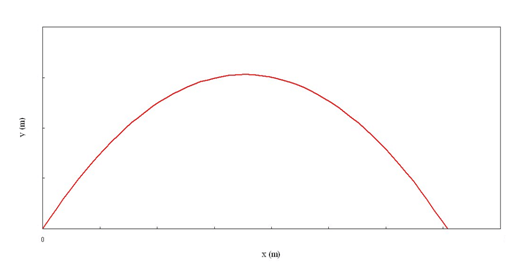
Scriviamo le due equazioni lungo x ed y che descrivono la traiettoria:

Calcoliamo le componenti x e y della velocità iniziale dell'elettrone:
Vox = Vo · cosα = Vo · cos45
Voy = Vo · senα = Vo · sen45
Calcoliamo l'accelerazione con cui viene frenato l'elettrone:
a = F/m = (E · e) / m
Dunque il sistema precedente diventa:
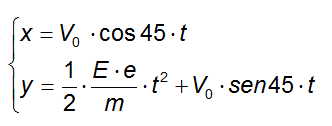
Ricaviamo t dalla prima equazione:
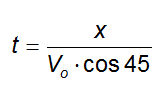
e sostituiamolo nella seconda:
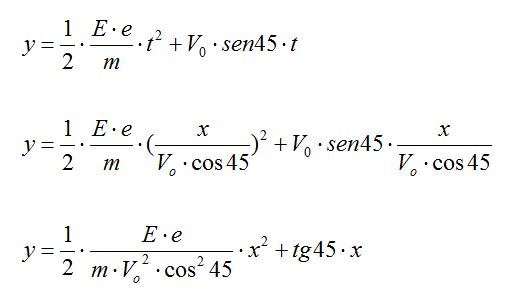
Ricordando che
cos 45 = ![]() / 2
/ 2
e
tg 45=1
si ha che:
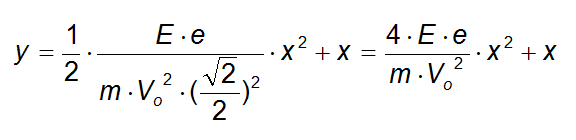
che rappresenta una parabola con la concavità verso il basso (e < 0) e quindi descrive la traiettoria dell'elettrone.
Bisogna ora verificare che il vertice di tale parabola abbia quota inferiore a d ed in tal caso l'elettrone non urterà l'armatura superiore e se il punto in cui taglia l'asse orizzontale sia superiore a L ed in tal caso l'elettrone non urterà l'armatura inferiore.
Il vertice di una parabola ha quota pari a:

Per cui essendo H > d vuol dire che l'elettrone potrebbe arrivare ad una quota massima superiore alla distanza tra le due armature, se il campo fosse esteso a tutto lo spazio, e quindi colpirà l'armatura superiore.
Per determinare dove questa verrà colpita imponiamo che y sia pari esattamente a d:

Scartando la soluzione negativa, otteniamo x = 2,7 cm.
Per cui l'elettrone colpirà l'armatura superiore a 2,7 cm dal bordo sinistro.
Studia con noi