Applicazione della relatività galileiana
Applicazione della relatività galileiana al moto di una barca
Una barca la cui velocità è di 10 km/h attraversa un fiume la cui corrente scorre a 5 km/h.
Il barcaiolo vuole procedere perpendicolarmente alle rive del fiume e quindi anche alla velocità dell'acqua.
Secondo quale angolo deve inclinare la propria imbarcazione, rispetto alla direzione perpendicolare alle rive, per ottenere questo risultato?
Calcolare la velocità rispetto al suolo.

Svolgimento dell'esercizio
Detti Vb e Va rispettivamente i due vettori relativi alla velocità della barca e dell'acqua, i due vettori risultano essere l'ipotenusa e un cateto del triangolo rettangolo che ha per cateti Va e la velocità V con cui sta procedendo la barca, velocità quest'ultima perpendicolare alle rive:
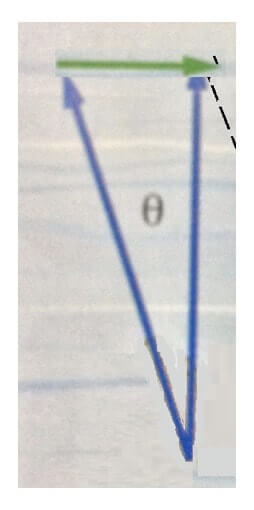
Per cui deve risultare che l'angolo θ da ricavare è legato per ragioni trigonometriche ai due elementi in nostro possesso dalla relazione:
Vb ∙ senθ = Va
senθ = Va / Vb
θ = arcen (Va / Vb) = arcsen (5/10) = 30°
Il modulo di V vale invece, per il teorema di Pitagora:
V = √(Vb2 – Va2) = √(100 -25) = 8,66 km/h = 8,66/3,6 m/s = 2,4 m/s.
Studia con noi